Draw Circle Using Distance Formula Cpp

Equation of a Circle

In geometry, a circle can as well be represented in the expanded form. It is the upshot of expanding the binomial squares in the standard grade and combining like terms. To find the equation of circle nosotros use the distance formula.

In this section, nosotros will learn the standard and full general course of the equation of a circumvolve, and too solve some problems based on it.

At that place are two forms of the equation of a circle:

• Standard Grade
• General Form

Standard Form

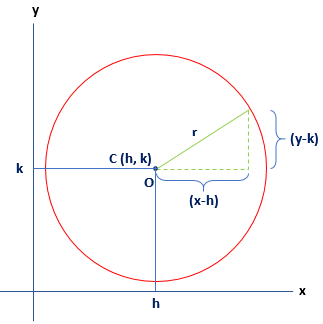
If the equation of a circle is in standard grade, nosotros can easily find the center of the circle (h, k) and the radius of the circle. The standard equation of a circle is:

(x-h)ⁱⁱ+(y-thou)²=r^two

Where (h, yard) is the coordinates of the heart, and r is the radius of the circumvolve. Remember that the value of r is ever positive.

Allow's run across some examples based on the standard form.

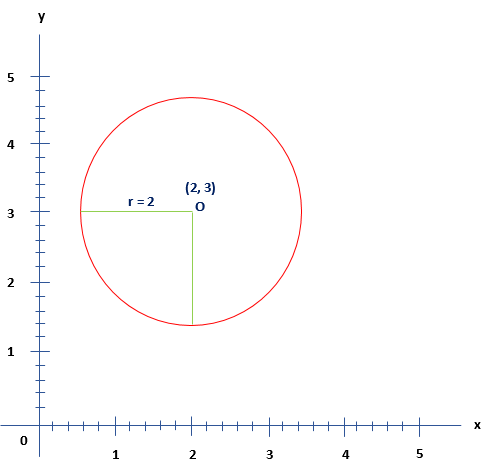
Example one: Find out the radius and center of a circle from the given equation. Too, draw the graph.

(x-2)²+(y-3)²=iv

Solution:

The given equation is, (x-2)²+(y-3)²=4.

Remember: If the minus sign is preceding the (h, m), (h, yard) will be positive.

Compare the given equation with the standard form, we get:

h=2,k=3 and r²=iv
r=√4=2

Now, we can plot the circle on the graph paper with radius r = 2 and centre (2, 3).

Instance 2: Find out the radius and center of a circumvolve from the given equation. Besides, depict the graph.

2xⁱⁱ+2y²=eight

Solution:

The given equation is, 2x²+2y²=eight

The higher up equation is not matching with the standard form. So, first, we convert the equation in the standard form by dividing the equation by 2.

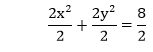
Solving the in a higher place equation, we get:

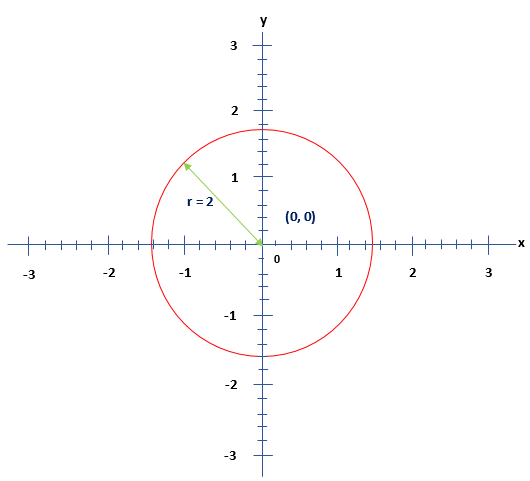
ten²+y²=four

Nosotros tin write the above equation equally:

(ten-0)²+(y-0)²=4

Compare the above equation with the standard course, we get:

h=0,thousand=0 and r²=4
r=√iv=2

Now, we can plot the circle on the graph paper with radius r = two and center (0, 0).

Example 3: Notice out the radius and center of a circle from the given equation.

(10-4)²+(y+5)ⁱⁱ=81

Solution:

The given equation is, (x-iv)²+(y+5)²=81.

Compare the given equation with the standard form, nosotros get:

h=iv,k=-5

Nosotros run into that y coordinate is negative. In general, y term is (y-grand)^two. Nosotros have given that (y+five), so grand must be negative. We tin also write it as: (y-(-five))ⁱⁱ. Hence, y coordinate is negative.

Hence, the coordinate of the center is (4, -5) and the radius of the circumvolve is 9.

r²=81
r=√81=9

Case 4: The radius of a circle is 25 cm and the eye coordinate are (-two, 6). Write the equation of the circle.

Solution:

Given, radius (r) = 25 cm

Center coordinate (h, k) = (-ii, 6)

(x-(-2))²+(y-6)^two=25
(x+2)²+(y-6)^two=25

Hence, the equation of the circle is (ten+2)²+(y-6)²=25.

Example 5: Write the equation of the circle given below.

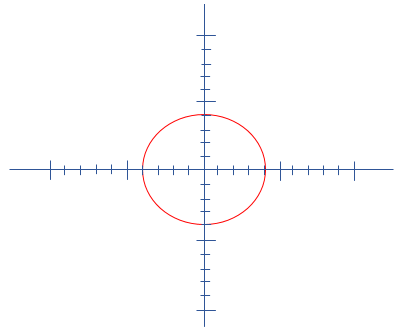
Solution:

In the given effigy, the center coordinates (h, one thousand) are (0, 0) and the radius (r) is four. Hence, the equation of the circle is:

x²+y²=16

General Form

The general form of the equation is the expanded form of the standard equation. We know the standard equation of the circumvolve:

(x-h)^two+(y-k)^two=rⁱⁱ…………(one)

Expanding the equation (ane), we get:

x^two+h²-2hx+y²+one thousand²-2ky=r^two

Rearrange the to a higher place equation, we become:

x²+y²-2hx-2ky+h^two+yardⁱⁱ=r²
tenⁱⁱ+y²-2xh-2yk+h²+k²-rⁱⁱ=0…………(ii)

Substitute the values of h, m, and r by the post-obit values, we go:

h=-g,one thousand=-f,c=h²+k²-r^two

Put these values in the equation (ii), we become:

tenⁱⁱ+y²-2x(-g)-2y(-f)+c=0

Where (-g, -f) is the center of the circle, and the radius (r) is √g²+f²-c^two .

10²+yⁱⁱ+2gx+2fy+c=0

Where one thousand, f, and c are constants.

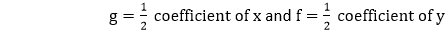
We can further substitute the values 2g, 2f, and c by D, E, and F, respectively.

x²+y²+Dx+Ey+F=0

Where D, E, and F are constants.

Note

• If the value of g²+fⁱⁱ-cⁱⁱ>0, the radius of the circumvolve is real and the equation represents a existent
• If the value of 1000²+f²-c²=0, the radius of the circle also becomes 0. In the particular case, the circle reduces to the bespeak (-1000, -f) and the circle is chosen a betoken circle.
• If the value of g^two+fⁱⁱ-c²<0, the radius of the circle becomes imaginary. But the circle is not imaginary, information technology is existent. This type of circle is called an imaginary circle.

Let'south solve some examples based on general form.

Example 6: Find the center coordinated and radius of the circle from the given equation.

4x²+4y^two-16x+24y-36=0

Solution:

The given equation is 4x²+4y²-16x+24y-36=0.

Start, we will divide the whole equation past 4, nosotros become:

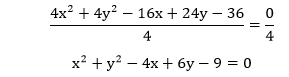
Rearranging the above equation, we get:

10^two-4x+y²+6y=9……(1)

At present nosotros will find the value of chiliad and f, respectively.

We know that,

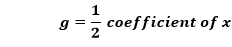
In the in a higher place equation, the coefficient of x is -4. Therefore,

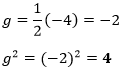
Similarly, we volition find the value of f. Nosotros know that,

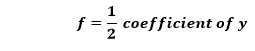
In the higher up equation, the coefficient of y is 6. Therefore,

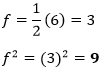
Note: We add together the value of yard^two and f² to both sides of the equation.

Putting the value of g and f in the equation (i), we get:

(x²-4x+4)+(y^two+6y+9)=9+four+9
(10-ii)²+(y+3)²=22

Compare the to a higher place equation with the standard grade, nosotros get the middle of the circle and radius of the circle.

h=ii,grand=-3 and r²=22
r=√22=4.7

Hence, the center of the circle is (2, -three) and the radius is 4.7.

Example 7: Detect the middle and radius of the circle from the given equation.

x²+y²+2x+4y-9=0

Solution:

The given equation is: ten²+y²+2x+4y-9=0.

Rearranging the higher up equation, we get:

10^two+y²+2x+4y=9
x²+2x+y²+4y=ix……(i)

Now we will find the value of g and f, respectively.

Nosotros know that,

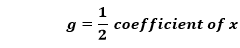
In the above equation, the coefficient of ten is 2. Therefore,

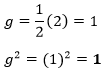
Similarly, we will find the value of f. Nosotros know that,

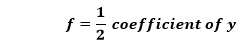
In the above equation, the coefficient of y is 4. Therefore,

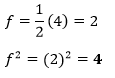
Note: Nosotros add the value of g² and f² to both sides of the equation.

Putting the value of chiliad and f in the equation (i), we get:

(x²+2x+1)+(y²+4y+4)=9+one+iv
(x+1)ⁱⁱ+(y+two)²=14

Compare the in a higher place equation with the standard form, nosotros get the centre of the circle and radius of the circumvolve.

h=-one,1000=-2 and r²=14
r=√14=3.8

Hence, the heart of the circle is (-i, -2) and the radius is iii.8.

---

foxworthdindoutiors.blogspot.com

Source: https://www.javatpoint.com/equation-of-a-circle

Share this post